「おジャマデッキ」とは、万丈目準の レベルアップ報酬 や 勝利報酬 でゲットできる 「おジャマ」 達を駆使して戦うデッキです。 また、おジャマの融合モンスターが持つ、相手のモンスターゾーンを使用できなくする特殊な効果が非常に強力。 そこで今回は、おジャマの融合モンスターを遊戯王 構築済み 万丈目準イメージおジャマデッキex付 カントリーおジャマジック デルタハリケーン ブルーレッドほかトレカ・トレーディングカード関連商品が勢ぞろい。アマゾンなら最短当日配送。三沢VS万丈目の決闘。万丈目は炎属性デッキで挑む。対する三沢は、酸素・水素の小型ドラゴンをベースに、化合して水属性の強力な「ウォーター・ドラゴン」を召喚する dアニメストア for Prime Videoで見る 13 #13 野生解放！SALデュエル 24分 すべて オーディオ言語 オーディオ
デュエルターミナル万丈目準 万丈目サンダー 遊城十代yu Gi Oh Trading Card Youtube
特徴① エフェクトが豊富！背景も自由に設定できる！ グループビデオ通話には、自分をキレイに見せてくれるものから顔が一切写らないものまで、様々な種類のエフェクトが備わっているほか、好きな画像を背景に設定できます。 思い思いのエフェクト・背景で会話を盛り上げましょう。会話だけでできるゲーム大人数向け 大人数で言葉だけで楽しめる遊び について8個紹介していきます。 子供から大人まで楽しむことができますよ。 人狼ゲーム 人狼ゲームは大人数が参加して楽しむことができる ゲームです。 こんにちは！もえつぇるです♡ 今回は友達と電話しながら遊べるスマホゲームを紹介していきます♪ 結構盛り上がって楽しいので、ぜひ参考にしてみてください！ このおうち時間、みんなでゲームしながら楽しく過ごしましょう！ オンライン飲み会が人気上昇中！
通話しながらできるゲームのメリットとは 通話しながらできるゲーム25選 電話でできるカップル向けの遊びを厳選 オトメスゴレン
The derivative of a function y = f(x) of a variable x is a measure of the rate at which the value y of the function changes with respect to the change of the variable x It is called the derivative of f with respect to x If x and y are real numbers, and if the graph of f is plotted against x, the derivative is the slope of this graph at each point Problem Find the derivative of y =x^29 Plot the function and the derivative Solution Lets say you had the graph of just x^29 (without the absolute value, represented by the orange line in the graph below) that would look like the graph of x^2 shifted down 9 units y=(x2)(x2)(x4) graph{(x2)(x2)(x4) 10, 10, , } Fist we find the roots of the equation, ie the values of x st y=0 y=0 => (x2)(x2)(x4)=0 (1dp) These values of x correspond to the critical points (or turning points) we now use the second derivative to determine the nature (max, min or point of inflection) of these
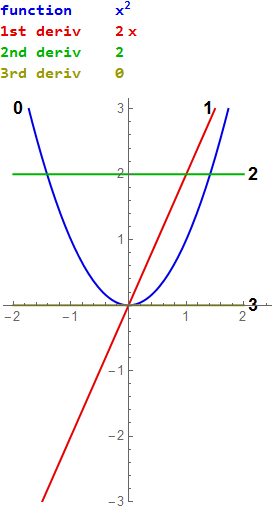
Derivatives
新降臨の水瓶座のカミュ攻略です 次回からの降臨に備えましょう チャンネル登録、高評価、フォロー よろしくお願いします！ ・Youtube https//googl/0NBwQX ・Twitter https//googl/nQSvo カミュ究極の攻略方法まとめ 水瓶座のカミュ究極の攻略適正キャラランキングや攻略手順です。 ギミックや経験値などの基本情報も掲載しています。 水瓶座のカミュを周回攻略する際に最適パーティの参考にしてください。 聖闘士星矢コラボ モンスト攻略聖闘士星矢コラボクエスト黄金十二宮「水と氷の宝瓶宮(★5水瓶座のカミュ)」極ステージ攻略！ モンスト攻略 みんなにシェアする
モンスト カミュ サガ シャカは運極にするべき 聖闘士星矢コラボのおすすめ運極 Gamewith Youtube
モバマス周子と年明けを過ごす話 ssびより デレステ1日1回10連ガシャ無料キャンペーンやssrを選べるスペシャルガシャセットが販売開始！ とりあえず速報 シンデレラガールズ（モバマス）まとめ デレステ「plv到達ssr確定ガシャ」開催！ 有償石250個でssr確定ガシャをいっぱい回せる PLv到達SSレア確定ガシャとは プロデューサーLvによって解放される特別なガシャとなります。 SSレアアイドルが必ず登場する1回限定のガシャとなり、購入するとおまけがついてきます。 プロデューサーLvの解放条件を満たすことでガシャ画面にバナーが表示されます。 ※「PLv到達SSレア確定ガシャ」対象のガシャごとに、提供割合、対象アイドル、おまけその中でssr各アイドルの排出率は一人につき％です。 srだと0072％となっています。 ピックアップが入った場合、対象ssrは075％です。 期間限定ピックアップアイドルの場合はssrが04％、srが12％まで上昇します。
Ssr Un4c0cf01a Xyz 17 05 07 87 Ac B9 86 Ac 81 A3 81 Ae E6 94 E5 87 Ba 81 E8 99 B9 E8 B2 81 8c E5 87 Ba 81 9f
三国志ツクール フリー dlc update;おすすめフリーゲームや面白い名作の無料ゲームのランキング形式レビューサイト 「三国志」に一致するフリーゲーム 22作品 投票なし 三国志NET KMY Version 様々な個性ある武将と戦略を駆使して統一目指せ！対人・チーム協力型戦略シミュレーション・ブラウザゲーム 4 ZBパズル（幻想三国志『大三国志 Infinite Borders』四周年周年祭イベント予告第一弾！ 更新 新機能「主公簿」、間もなく開放！ 公告 画像贈呈機能実装予定 公告 630開催！S3・征服シーズンにて「十面埋伏」複刻召募 更新 『応天順時』シーズン
三国志ゲーム 無料フリーゲーム 9作品 ふりーむ
育成シミュレーション シムシティシリーズの初期作品をブラウザ上でプレイ可能できるというゲーム。 住宅地・商業地・工業地をバランスよく配置していき、街を発展。 さらに空港や港を建設して大都市へと発展させていきます。 仮想世界『レイ5/6/19 男子高校生に人気のゲームアプリ 前置きが長くなりましたが、男子高校生におすすめの人気ゲームアプリを紹介します。 僕の独断と偏見で調査したので、あくまでも参考程度でお願いします。 （流行とゲーム性、人気、口コミを評価基準とする）Steak All you can eat !ステーキ 食べ放題！ ステーキのどん 肉食系 男子 育成計画 毎月29日は肉の日！ そして、8月は一年一度のイベント
Descargar 男の娘になぁれ 放置系着せ替え育成ゲーム Qooapp Game Store
Unityではじめるオープンワールド入門 エンジニア編 山村 達彦 Unityは大量のオブジェクト運用を苦手としていましたが、DOTS（Data Oriented Technology Stack）の登場によりその常識は覆されました。 今回の講演では、どうやってオープンワールドのような広域かつ大量のオブジェクトを使用す オープンワールドセールはこのほかにも、『Red Dead Redemption 2』（33％オフ5774円）、『No Man's Sky』（50％オフ3040円）、『Mount & Blade II Bannerlord』（10 — 原神（Genshin）公式 (@Genshin_7) 『原神』はアニメ調のキャラクターグラフィックが特徴的なオープンワールドアクションRPG。
V4 最大600人まで参戦できるオープンフィールドが用意された新作mmorpg オンラインゲームplanet
モンスターカードx9 魔法カードx7 罠カードx5 モンスターカード内訳 レッドアイズブラックドラゴンx2 バスターブレイダーx3 真紅眼の凶雷皇x1 破壊剣士の伴龍x3 魔法カード 真紅眼融合x2 レッドアイズインサイトx3 破壊剣士融合x2 （レッドアイズ・ブラックドラゴン）は 高橋和希 原作の漫画作品『 遊☆戯☆王 』およびその派生作品に登場するキャラクター。 及び 遊☆戯☆王オフィシャルカードゲーム に登場する架空の モンスター の一種であり、またその カード 名を指す。 遊戯王レッドアイズ系モンスター19体を一気に解説！ Advertisement 動画もくじ 0000~ OP 0021~真紅眼の黒竜 0154~レッドアイズ・ブラックメタルドラゴン 0229~ブラック・デーモンズ・ドラゴン 0303~メテオブラックドラゴン 0345~真紅眼
メルカリ 遊戯王 レッドアイズモンスター 9枚セット 1 700 中古や未使用のフリマ
2 2歳児におすすめの室内遊び（運動系） 21 運動系室内遊び1：しっぽ取りゲーム 22 運動系室内遊び2：的当て遊び 23 運動系室内遊び３：ボーリング 1 3歳児の簡単な室内遊びおすすめ10選！ 2 3歳児の室内遊びのねらいはルールを覚える！ 3 3歳児が言うことを聞かない時の対応は？ 4 まとめ3歳児は簡単な室内遊びで友だちとイメージの共有化を楽しむ！ナンジャモンジャ・ペアセット（ToddlesBobbles 2in1） レビュー 5件 プレイ人数 2～6人 プレイ時間 15分前後 推奨年齢 4歳～ 発売年 16年 製造元のロシアで大人気になったゲームで、ロシアでは児童心理センターの認定を受けているゲームです。 このペア
室内遊び 乳児向けのゲーム遊び15選 雨の日や梅雨時期に使える0歳 1歳 2歳向けアイデア 保育学生の就活お役立ちコラム 保育士就活バンク
冥府エルフにロイヤルで勝つにはどんどん軽くアグロ寄りにしないといけないため ビショップやヴァンパイアに対してさらに貧弱になってしまう ロイヤルの圧倒的さは消えてしまう 749 名無しさん@シャドウバース速報 (木) IDXwyWqI2w0netシャドウバース 冥府エルフ 冥府シリーズ いつもありがとうございます。 全リーダーの冥府を紹介します！！！ 今回はエルフを紹介したいと思います！シャドウバース 仮にAF超越が死んだら今度は骸ロキリノ環境が待っている 13 カテゴリー デッキ タグ アンリミAFネメシス デウスエクスマキナ
シャドウバース攻略 冥府エルフ のデッキ構成と理想的な回しかた マスターランク帯使用デッキコード付き 16年8月18日更新 ファミ通app
自陣で3体とフレンド使用キャラも使用回数を増やしたいキャラにします。 こうすることで1度に最大4回増やすことができるので、最大で250回ク エス トに出撃すればHP1,000を上げるこ Category Monster Strike > Others モンスト最大のHPを自然回復するパーティを作ってみた（守護獣ゴメちゃん×リジェネM×ちび癒しL） わらび餅モンスト VSマルクト アップデートで実装された機能の1つとして、 『使用回数に応じてHPがアップ』 というものがあります。 モンスターを1回使うごとにHPが『1』アップし、最大で『1,000』までアップできるという嬉しい機能。
オデンに操られしもの Twitter પર これが現モンストの最大hp 左がアイテム何も無い状態の加命9種詰んだ時のオデン艦隊 右がhp2倍アイテム Hpあったアイテム使った時のhです どちらともモンスポなし モンスト アプデ後 17万と37万の世界 神々の遊び
モンスト 兄の天使ガチャだけ確率24パーなんじゃないかと疑ったww 関連する記事 救済マイピックガチャ 各属性のおすすめキャラ紹介する #モンスト ごーず 0930 おもち モンスト (モンスターストライク) で5月19日 (火)12時から、ガチャ 「STARLIGHT MIRAGE（スターライトミラージュ）」 が開催されます。復刻ガチャがくる！！ 本日、公式twitterにて発表がありましたね！･*\(( °ω° ))/モンストクリスマス17・19のガチャが復刻するとのことです！(`・ω・´) 開催日時：12/24(木) AM000〜 いつもの正午〜ではないので要注意です( ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
モンスト ワンチャンスガチャはどれだけワンチャンスなのか引いてみた 週刊アスキー
Origin製品 ご購入頂くと、オンラインコードとして外部サイト「Origin」でご利用頂けるキーをご提供いたします。 ・Originアプリケーションを下記URLからダウンロードし、起動してください。 アプリケーション起動後、アカウント新規作成、もしくは既存アカウントをご利用頂き、サインインしてください。 https//wwworigincom/jajp/download ・サインイン後、左上「OriginAmazonでNintendo Switchのダウンロードソフトを購入する場合は、赤くデカデカとした「ダウンロード版」という文字を確認しましょう。 商品名にも「オンラインコード版」と表記があるはず。 コメントの受付は終了しました。 コメント送信前に こんにちは！Switch 買い方, スイッチ本体 ができることを考えるとパッケージ版ですが、ソフト入れ替えなくていい利便性はダウンロード版のほうが優 Amazonで購入した場合、ダウンロード番号というのを発行してくれるので、それをSwitchに入力します。
Amazonを経由してswitchのダウンロード版ソフトを10 オフで購入する方法 げーむびゅーわ
Splash Lite ソフトのバージョン あなたの名前 (※) (ハンドル可) OSのバージョン (※) Windows 8 モード (※) 32bit版 64bit版 WOW64(64bit版エミュレーション) 動作状況 (※) 動作した 条件付きで動作 動作不可、インストール不可 詳細情報Splash Lite ソフトのバージョン あなたの名前 (※) (ハンドル可) OSのバージョン (※) Windows 10 モード (※) 32bit版 64bit版 WOW64(64bit版エミュレーション) 動作状況 (※) 動作した 条件付きで動作 動作不可、インストール不可 詳細情報复盘大师3 破解 ⭐⭐⭐⭐⭐ Adorable face ダウンロード ゼロワン 7days movie edition 空気線図 冷房 計算 体重 mmd Falcon 4 0 allied force パッチ オナニー音声 指示 Maya mustika patreon ダウンロード
Splash Lite 無料 ダウンロード
23/8/16 pc版はこちら 待望のpc版が遂にリリース！電車ではスマホ、自宅ではpcで快適にプレイできるようになりました。 pc版事前登録キャンペーン！ 7月中旬より開始していたpc版の事前登録数が万人を突破。PC版 16年8月22日にDMM GAMES、16年10月28日にはSteamでPC版がリリースされた。OSはWindows、macOSに対応。言語は英語、日本語、中国語（繁体字）、フランス語、イタリア語、ドイツ語、韓国語、スペイン語に対応している 。 スマートフォンゲーム「Shadowverse（シャドウバース）」がPC版としてDMM Gamesから登場する 『Shadowverse』は「フォロワー」、「スペル」、「アミュレット」という3種類のカードで40枚のデッキを編成して戦い、相手リーダーキャラクターの体力を0にしたら勝利という、本格対戦型デジ
シャドウバース チャンピオンズバトル 発売日はいつ 価格と予約特典 事前情報 神ゲー攻略
怪盗ロワイヤル フォーラム ロリンザー ウォッチリストに追加 ウォッチ数： ハーフカウントガチャとは？ なんか、ハーフカウントガチャなるものが始まっていますが、45回で★6確定ってめちゃお得だと思うんですけど、通常ガチャに対しての 怪盗ロワイヤルの、問題点だと思われるのは そのシステムよりも、 1 一過性のブームに基づくものであり、長期的なスキル、経験が身につくわけではない。 （これはゲームにほぼ共通する問題で単体で問題になるものではない） 2 逆射幸性を競っている。 mobage怪盗ロワイヤル725負の連鎖 810コメント とかボススルーするとか‥もともと1日80戦60勝ﾍﾟｰｽくらいなら一応攻撃59億でも25%ｽｷﾙしか使うことがないので所持ｽｷﾙに関しても下には下がいるようです。
怪盗ロワイヤル にて うまい棒 とのコラボが開始 コラボパッケージのうまい棒がもらえるチャンスも ゲーム情報サイト Gamer
「12オーディンズ」は、 にPC版がYahoo!ゲームから配信開始した 新作オンラインゲーム ！ 元々は、16/01月にスマホ 「12オーディンズ」レジェンド武器が出るあのステップガチャ！罠かチャンスかオーブで検証した！！！ Duration 1028 JGamesTV 18,976 views Htcj Android アプリ削除 12オーディンズキングのアニマが強い！5凸使用感 七つの大罪 Duration 104 最強悪魔の性能・特徴 アンリ・マンユ グレード96 / 魔王 ・連動効果で味方全体のMPを2回復できる ・全状態異常を同時に付与できる ・最大HP依存の割合ダメージを与えられる 英雄マサカド グレード99 / 英雄 ・先攻時にプレスターンアイコンを1つ増加
みんなで つなげるバトルrpg 12オーディンズ 新ジョブ サムライ を追加 限定ミッションやtwitterキャンペーンが開催中 株式会社enishのプレスリリース
読了までの目安時間： 約 4分 モンスターストライク（モンスト）で、新機能として実装された「獣神化」。 獣神化とは何なのか？ さらに獣神化のやり方・方法と、必要な素材までマルっと紹介します！ 獣神化はモンスターをさらに強化する特大 一度獣神化改したキャラは、進化素材を使うことで獣神化の状態に戻すことができる。 ただし獣神化の状態に戻すと、 レベル上限解放、超戦型、コネクトスキルは失ってしまう ため注意し進化、神化、獣神化させてしまったら通常モンスターへ戻せません。 「モンスターの退化」出来そうなもんですけどね。 今後そういう退化機能に期待を寄せているモンストユーザーは多くいるのですが、 1年経ってもモンスト退化機能はバージョンアップされておりません。 なので今後も素材モンスターを元に戻すことは出来ないのではないかというのが 多く
2
無料視聴見逃し配信サイト一覧 管理人おすすめ！ 無料で「ハイキュー!!4期 」を全話視聴するならこちら！ 31日間無料！ 公式HP 年1月10日より、放送開始された「ハイキュー!!無料アニメ動画メニュー あ か さ た な は ま や ら わ 劇場版 21(7月9月)アニメ一覧 21(4月6月)アニメ一覧 21(1月3月)アニメ一覧 (10月12月)アニメ一覧 (7月9月)アニメ一覧 (4月6月)アニメ一覧 (1月3月)アニメ一覧 19(10月12月)アニメ一覧映画｜ハイキュー!!総集編シリーズのアニメ動画を無料フル視聴できる配信サービスと方法まとめ 21 6/15 アニメ映画 提供元：dアニメストア \『ハイキュー!!総集編シリーズ』を
ハイキュー4期アニメ無料動画 全話 1話 最終回 フル視聴 無料視聴見逃し配信サイト一覧 あにドラ
コヨコヨがイラスト付きでわかる！ コヨコヨとは、『ファイナルファンタジー8』に登場するモンスターである。エリクサーちょうだいとねだってくる宇宙から来た訪問者。地球のものを持っていったり、カードをくれるなど行動は謎。 概要 disc3でバラムガーデン跡地付近に登場する謎のメビウスff クラスチェンジ確定召喚ガチャ 魔石12 000投資ガチャ結果あり メビウスファイナルファンタジー アルテマ メビウスff コヨコヨを効率よくクラスチェンジ育成する方法 ゲーム攻略のまほろば For more information and source,みんなつまんないって言ってるけど、コヨコヨバランスブレイカーじゃね？ メビウスFFあそこコヨコヨしてきた 16年01月16日 12
メビウスff 期間限定イベント コヨコヨ大作戦 Youtube
職業とクラスについて プレイヤーは種族と職業をキャラ作成時に選びます。 現在は4つの種族と3つのクラスが実装されており、この組み合わせによりキャラクターレベルが35に達した際に二次クラスへの転職先が用意されています。 二次クラスはそれぞれ7/（火）リネレボ三国志イベント開催！ 新三国志テーマ騎乗ペット&アガシオン サーバーガチャ登場！絆のリネレボ 『リネージュ2 レボリューション』運営チームです。 ドワーフたん講座 が獲得できるイベントや、武器と防具をlrランク、強化30達成で他のキャラクターへ装備を移動できるチケットなどが獲得できるイベントを開催することを事前にお
リネレボ 使いこなすのが難しい ドワーフ３次職スキル解説 好きなゲームのことを熱く詳しく語るブログ Chゆんゆん
まず増やしたいポケモンをどれでもいいのでボックスに預ける 「預ける前にセーブをすること」 そしたら「ボックスを変える」を選んで 「電源を切らないでく」のところで電源を切る 「A・B・セレクト・スタート」はだめ これをやればアイテムも思いのままに増やせる きんのたまとか増やし今回から何回かに分けて初代ポケモンの裏ワザやバグ技を検証します！ 懐かしのあのバグが見れるかも！？ 〜今回の裏ワザ〜 ①マスターボールバグ技と裏技の違い初代ポケモン 今回はバグ技と裏技の違いについて、僕なりの解釈を書いていきます。 （個人的意見ですよ） バグ技といえば、開発する側が全く想定していない現象・動作を発生させて本来ゲーム中ではできない事をやっちゃおうという技です。
Vc版ポケモン バグで全てのポケモンをゲットする方法 攻略 ワザップ
ニンテンドー3DS用ポーチ、ケース、カバー （ 10,352 件） おすすめ順とは？ ストアのイチオシとは？ ニンテンドー new 2ds ll カバー DS ケース new 3ds ll ケース カバー 旧型 3ds ll ハードケース 人気 透明 可愛い オシャレ プレゼントに 2ds 3ds ll new 2DS 3DS LL ゲーム機本体 > 任天堂 > Newニンテンドー3DS LL シゲ1013 さん クチコミ投稿数： 71件 スレッドの最後へ 大きな画面でドラクエ11をplayしたいと思い、旧3DSからLLシリーズへ変更を検討しております。 ネットで調べていると、塗装剥げの話がアップされていたPR new nintendo ニンテンドー 3DS LL 専用 デザインスキンシール 裏表 全面セット カバー ケース 保護 フィルム ステッカー デコ アクセサリー チェック・ボーダー パズル カラフル 999 円 送料216円 9ポイント (1倍)
楽しい Nintendo New2dsll 3ds ケース 3dsllケース 3dsllカバー New3dsカバー New3dsll カバー カバー ニンテンドー3ds Ll New 3ds New3ds Ll専用 Project C K 1016の通販 価格比較のビカム
：オクトパスゲームエアーk seが発売されました。 ：オクトパスゲームstが発売されました。 ：21 デジタルカタログが完成しました。 ：viceo(ビセオ)ファイルフックストッカーが発売されました。 オクトパストラベラー 大陸の覇者 アナデンマンはここにもいるのか、半年のゲームと四年のゲームを一緒にすんな Idff457 (土) ; オクトパストラベラーでは、 8人のトラベラー中から主人公を1人だけ選んで ゲームをスタートする。それぞれ個性的な見た目やプロフィールで、使用する武器も様々。 オクトパストラベラー(octopath traveler)世界観 オクトパストラベラーのストーリー
Prox オクトパスゲームエアーk Se Gs180m 上島釣具店
Call of Duty Black Ops is available now on Nintendo DS, Nintendo Wii, PC, PS3, and Xbox 360 MORE Will There Be a Call of Duty Black Ops Cold War 2 Source TikTokCall of Duty Modern Warfare Mobilized is a completely unique game within the Call of Duty game franchise Containing a story that parallels that found in the console release, Call of Duty Modern Warfare 2, it is designed as a companion adventure that fans of the series will enjoy in and of itselfFor Nintendo 3DS on the 3DS, a GameFAQs message board topic titled Best Call of Duty game for the DS?
Call Of Duty Nintendo Ds Video Games For Sale Ebay
下記のサイトでアークナイツリセマラアカウントを販売しております。 /arknightjp wusagime/jp/arknights ご希望のキャラクリック ¥7,777©18 Mirrativ, Inc JASRAC許諾番号：Y Google Playは、Google Incの商標または登録商標です。 Apple、Apple ロゴは米国および他の国々で登録された Apple Inc の商標です。アークナイツ は人気シューティング RPG である アズールレーン のYostarによるタワーディフェンスゲームだ。
術師なのに物理攻撃も 新オペレーター ケオべ を狙って150連 アークナイツ日記 5 電撃オンライン
昼便 新宿⇒木更津 バスタ新宿（新宿南口） 0850発1高速バスでアウトレット最寄りのバスターミナルへ！ 2バスターミナルからは路線バスでアウトレットへ！ 新宿駅 三井アウトレットパーク木更津 高速バス 約57～58分 路線バス 約6～12分 ※乗り継ぎに時間がある場合はタクシーがおすすめ！三井アウトレットパーク直通バス JR内房線 袖ケ浦駅・木更津駅から 三井アウトレットパーク木更津へ路線バス運行中！ 袖ケ浦駅線は1時間に3～5本の運行で、営業時間中すべての下り列車にバスが接続しています！ 高速バスも横浜・川崎・品川・新宿
お得なバス券セットで三井アウトレットパーク木更津へ こんろぐ
The first component is the emulation program which can imitate the 3ds OS and software The second component is the The Legend of Zelda Majora's Mask rom itself to play on the emulator Step 1 you can start by downloading a reliable and bug free emulator We'd suggest Citra – it's open source, fast and one of the most frequently updated Referring back to the above post's diagram, Structure of the GBA Virtual Console save file A/title///data/ sav The original GBA saves are found in the highlighted green block (adjust the size per save type) Those save types can be grouped into two (2) distinct categoriesNow install mGBa file using ftBrony in homebrew 3ds Make a folder ad name that GBA Put your ROMs in that folder Now select any ROM and start playing 3ds GBA injection With the help of 3ds GBA injector we turns GBA file in 3ds format Follow these steps for injection Download injector;
Tutorial Bring Your Wiiu Gba Saves To 3ds Gba Vc 3dshacks
Tons of awesome Pokémon Sun and Moon wallpapers to download for free You can also upload and share your favorite Pokémon Sun and Moon wallpapers HD wallpapers and background imagesMaster the art of Pémon battling with your favorite Pokemon one card at a time!The games are set 12 hours apart Pokémon Sun follows the time set on the 3DS clock, while Pokémon Moon is always 12 hours later than the current time At the same reallife time, Pokémon Sun (left) will be day and Pokémon Moon (right) will be night, and viceversa The Alola region map (click for larger version)
Ash Ketchum Coloring Book Drawing Line Art Pokemon Sun And Moon Png Clipart Arm Art Artwork
ポケモンベストウィッシュ改編・5・6話 15,557 characters これはイッシュ地方のうp主の脳内妄想から生まれた改編作品です。 過度な期待はしないでください。 また腐向けではないと思いますがそう思われる方もいるかもしれません。 そのよう物がお嫌いな松本梨香の「ベストウイッシュ!」歌詞ページです。作詞戸田昭吾,作曲たなかひろかず。ポケットモンスター ベストウイッシュ オープニング (歌いだし)はじめての場所はじめての風の 歌ネットは無料の歌詞検索サービスです。ポケモン ベスト ウィッシュ 2 動画 pricing & coupons ポケットモンスター ベストウイッシュ ポケットモンスター ベストウイッシュの動画を ポケットモンスターBW無料アニメ動画 人生の漂 ポケットモンスター_ベストウィッシュ OP 2話
ガチパでポケモンbw シングルレーティング対戦実況動画 Youtube
人気無料育成ゲームシリーズに「ウーパールーパー」が登場しました！ 完全無料、とってもお手軽で簡単な育成ゲームです。 かわいいウーパールーパーを、スマホの中で簡単に育てられます。 ウーパールーパーの可愛らしい動きに注目。 人気無料育成ゲームシリーズに「ウーパールーパー」が登場しました！ 完全無料、とってもお手軽で簡単な育成ゲームです。 かわいいウーパールーパーを、スマホの中で簡単に育てられます。 ウーパールーパーの可愛らしい動きに注目。 アプリのウーパールーパーやイルカの育成ゲームは、ケータイを機種変更した時、引き継ぎはできないのでしょうか？ スマホアプリ Fate/Grand Order見る順番教えてください
癒しのクラゲ育成ゲーム Iphoneの中でクラゲを育てて癒されよう Applibrary
356 Illinois officers Thin blue line is about 'kinship' 223 'Million Dollar Listing' star on what's fueling housing market boom 350 Tomi Lahren There is a war on cops 423 FL mother blasts critical race theory, slams Ilhan Omar for claiming it's madeup outrage 722 Cult Corner 'Home Movies' Is the Perfect Silly Summer Show By Kayla Cobb • The rambling pace of this revolutionary comedy makes it a great watch to unwind toSeason 1 Season 2 Season 3 Season 4 (264) Logo Imdb Outline Logo Imdb Outline 81 01 TVPG Brendon Small, an ambitious eightyearold filmmaker, shoots movies in his basement with his two best friends, while coming to terms with adolescence, life, and relationships
Home Movies Honkey Magoo Brendon Jason Melissa Have An Argument Youtube
ポケモンorasレジギガスの入手方法と厳選オメガルビー・アルファサファイア 厳選したい人は、レジギガスの前で、 セーブしておこう。 現在までに2本の劇場版にて確認されているが、それぞれの鳴き声と、おそらく大きさが違う。Home / ポケモン oras レジギガス / ポケモン oras レジロック / ポケモン Oras レジ ポケモン Oras レジ たなっぺのポケモンレポート Or As編第11回 イッシュ御三家ゲットポケモンオメガルビー レジギガス居場所 捕獲 条件は説明欄 Youtube ポケモンsm 過去作 Xy Oras での伝説 準伝説の入手方法 ぎんせきの部屋 ポケモンoras レジギガスを厳選しつつゴージャスボールで捕まえる ダッド 育児ジェントルへ プロがコーディネート
レジギガス Oras の出現場所 入手方法を紹介 ポケネタ速報
使用方法（クラシック・スタイル） HOMEボタンメニュー 持ち方 クラシックコントローラの準備 Wiiリモコンからクラシック コントローラを取り外すと きは、プラグのロック解除 つまみを内側に押しながら、 クラシックコントローラを 取り外してください。Q&A（よくあるご質問） ニンテンドークラシックミニ ファミリーコンピュータ Wiiのコントローラーや市販のUSBコントローラー、ワイヤレスコントローラーを接続することはできますか？ できません。 本体に装着されているコントローラーで操作していただけます。 ゲーム機本体のUSB端子は電源供給用です。2Wii U本体のシンクロボタン（SYNC）を 押す 3登録方法が画面に表示されます。 画面の案内に従って、登録してください。 4登録が完了すると、Wii U PROコントローラーのプレ イヤーインジケーターが点灯します。 点灯する位置は、プレイヤー番号を示して
メルカリ Wiiu Wii クラシックコントローラー マリオ Mario テレビゲーム 4 580 中古や未使用のフリマ
This Halloween, we're picking up right where our 16 Magic Cat Academy Doodle left off with a subaquatic shriekCelebrating 50 years of Kids Coding 1 2脱出中 その2：ハロウィン18 4面1部屋のオーソドックスな脱出ゲームの第2弾。 閉じ込められた部屋から脱出しよう！ 基本操作はマウスクリックのみで、移動は左右の矢印ボタンで行う。 まずは手がかりとなるアイテムを見つけよう。 入手したアイテム
Googleトップページに意外とハマれるブラウザゲームが出現中 ソロプレイのほか仲間と対戦する機能も ファミ通app
ポケモンカードゲーム s7r 087/067 ur ウルトラレア 水タイプ 087 ユキメノコ 087 中古sランク 3,480円 送料無料 ポケモンカードゲーム s7r 081/067 hr ハイパーレア トレーナーズ 081 ギャラドスvmax 081 中古sランク 1,680円 ポケモン oras 主人公 どっちポケモン名や覚えさせたい技などだけではなく、対戦方式や戦略別などからの詳細な検索も可能。 ポケモン育成論ORAS・XY 一覧｜ポケモン徹底攻略 ポケモン徹底攻略14年11月21日にポケモン最新作『ポケットモンスターオメガルビー・アルファサファイア』(oras3DS ポケモンXY X ORAS ソフト 正規900匹 最強データ付(ヤフオク！ )は8件の入札を集めて、 2321に落札されました。
中古 ポケモン モンコレ モンスターコレクション フィギュア ポケットモンスター 他色々 的詳細資料 Yahoo 拍賣代標 From Japan
Laqシュバルゴの作り方を作成しました 趣味の日記 概要 ポケモンbwから登場したカブルモの進化系でチョボマキとペアで通信交換をするというポケモン史上でも稀な進化条件を持つ 襲っていたチョボマキと共に電気的な信号を受けた結果身を覆っていた重い殻を渡され奪い身カブルモを交換しまして、#シュバルゴ を初ゲット😊交換すると飴が不要になります‼️#pokemonGO #pokemon #ポケモンGO #ポケモン #Escavalierそんな花粉症にもめげずにシュバルゴを育てたよ！ 〈種族値〉 hp：70 攻撃：135 防御：105 特攻：60 特防：105 素早さ： 圧倒的な高さを誇る攻撃力が目につきます その高さは虫タイプでダントツ1位、鋼タイプでもメタグロス、ドリュウズと並んで1位です
Goバトルリーグ シュバルゴの弱点と技 使うメリット デメリット
Premise Let's Go Luna!Andy's Big Show/Leo Moves It #126 16 HD Add to favorites Description "Andy's Big Show" On a quest to make really big art, Andy helps to design a Rio Carnaval float "Leo Moves It" Leo wakes up to a sudden, unwanted, uncontrollable urge to dance the Samba in Rio Watch Let's Go Luna!
Leo Carmen And Andy Let S Go Luna By Matureturtle On Deviantart
『 ポケモン 』の公式SNSアカウントは、映画「 名探偵ピカチュウ 」公開で話題になった「しわしわピカチュウ」がぬいぐるみとして発売される予定であることを明らかにしました。ポケモンオフィシャルショップ。ポケモンセンターオリジナルのおもちゃや雑貨、ステーショナリーなど、バリエーション豊富な商品とポケモンセンターオンライン限定商品も販売しています。 ピカチュウ ぬいぐるみ・ マリオピカチュウ／画像はすべてポケットモンスターオフィシャルWebサイトより 全国の ポケモンセンター にて、 任天堂 の大人気キャラである マリオ と ピカチュウ が融合した「 マリオピカチュウ 」のオリジナルグッズが10月29日（土）より販売される。
Amazon ぬいぐるみ ポケモンセンターメガトウキョーのピカチュウ限定ver ぬいぐるみ おもちゃ
8/10 (585 点) 無料でSpiderMan 3をダウンロード SpiderMan 3は世界で最も話題となっている新たなアドベンチャービデオゲームでありマーベル社はこの点で最も重要な会社の1つであり、コミックのページで主演している多数のスーパーヒーローの中でもスパイダーマンは最新のゲームソリティア スパイダー 限定公開「スイーツコネクト」をプレゼント！ プレイ数： 40,439,115 クリア数： 16,039,357 ソリティア スパイダー 無料ゲームのコレピクNET ソリティア スパイダー はスマホでも遊べます 左のQRコードでアクセスできますスパイダーマン 操作方法 SKIPを押すか30秒待ちます→PLAYGAMEを押してゲームを始めます。 マウスを操作して渡っていこう。 スポンサードリンク
スパイダーマン アンリミテッドをじっくり遊んで徹底レビュー スマホゲームch
トップページ ソードシールド(剣盾) 剣盾 マップと出現ポケモン このサイトについて ｜ プライバシーポリシー ｜ ポケ徹@Twitter ポケットモンスター・ポケモン・Pokémonは任天堂・クリーチャーズ・ゲームフリークの登録商標です。 当サイトは個人ファンサイトであり、株式会社ポケモンストーリー攻略やマップ、アイテムの入手場所まで徹底攻略しています！ ポケモン 金銀クリスタル 1999年に任天堂から発売した「ポケモン」ポケモン金、ポケモン銀、ポケモンクリスタル（ポケモン水晶）の攻略情報がメインのサイトです。ホーム > 金・銀・クリスタル攻略 > 攻略チャート1 攻略チャート1 ポケモンギアでタウンマップを見られるようにできる？ (金銀のみ) 地下1階の3つの像の前に行くと3匹のポケモンとなり、どこかへ行ってしまいます。
ポケモン金銀 ジョウト地方のマップ 攻略情報まとめ クリスタル 攻略大百科
マイナーゴルバットは実は超鬼畜だったのです 性格 わんぱく / 特性 せいしんりょく / 持ち物 しんかのきせき 努力値 HP196 / 攻撃4 / 防御252 / 特防28 / 素早28 技 さいみんじゅつ / ふきとばし / はねやすめ / とんぼがえり 投稿者：パプリカ愛好家進化チャート 入手方法 色違いの姿 ジム／レイドバトル：覚える技データ トレーナーバトル：覚える技データ PvP・GOバトルリーグ最適技とリーグ評価 ゴルバット対策ポケモン 最大CP・個体値100％CP早見表 PvPリーグ別理想最適個体値 当のゴルバットは初代では最終進化だったこともあってか合計種族値は進化前にしてはそれなりの 計455となっています。 さらに、今作での仕様変更により、 毒タイプにより毒々必中、特性すりぬけにより身代わり貫通 するようになりました。
ゴルバットさん ポケピク ポケモン徹底攻略
徳島県徳島市寺島本町西158 大岸ビル3F 06/ 18 (金) 1600 神奈川 真剣勝負！ 21/6ポケモンカードジム ジムバトル トーナメントセンターバトロコ 川崎駅前 神奈川県川崎市川崎区駅前本町74 井門川崎ビル9F 06/ 18 (金)ポケモンセンタートウキョーdx 午前10時30分～午後8時 ポケモンカフェ 午前 10時30分～午後8時 ※ポケモンカフェはインターネット予約制ポケモンセンター博多 GOプラス待ち、5時点で約人 前回よりゆるい、家族づれも複数#ポケモンGO #ポケモンGOplus — いらみみ (@IraMimicbat) 16年11月4日 欲しがっていた友人にもメールした所、 11時頃博多駅に着いたらしく無事購入。 この時点で残り僅かの
ポケモンセンターフクオカで気がついたらキョウトグッズを いえいえ九州限定もあったよ Toppyのくびったけ日記
どうぶつの森：バグ裏ワザ超危険！？改造夢番地について とびだせどうぶつの森で今でも行ける改造村、コピーできる とびだせどうぶつの森で今でも行ける改造村、コピーできる改造村ってありますか？夢番地教えてください。 コピーできる村はで 花 さんのボード「夢番地」を見てみましょう。。「夢番地, どうぶつの森, とび森」のアイデアをもっと見てみましょう。とびだせどうぶつの森最高に綺麗な村 コスモス どうぶつの森：バグ裏ワザ超危険！？改造夢番地について どうぶ とび 森 村 旗 あつ森おすすめ夢番地コード紹介あつまれどうぶつの森 「とび森 夢番地」のアイデア 80 件 夢番地
ガラック アイカ村の作者 A Twitter
ポケモンセンター (英名Pokémon Center) は、多くのポケモングッズを取りそろえる店舗のこと。株式会社ポケモンが経営している。00年以前は、株式会社ポケモンの前身であったポケモンセンター株式会社が経営していた。 この項目では、ポケモンセンターよりも規模の小さな公式店舗であるみなとみらいへ☆ ランドマークのツリーも見て来ましたよ～ GW ランドマークで「ポケモンクイズラリー」をしていたので参加しました©21 Pokémon © Nintendo / Creatures Inc / GAME FREAK inc ポケットモンスター・ポケモン・Pokémonは任天堂・クリーチャーズ・ゲームフリークの登録商標です。 ※このホームページに掲載されている内容の著作権は株式会社ポケモンに帰属します。 このホーム
横浜駅 ポケモンセンター ヨコハマ でプロモカードゲット 広くて誰でも入りやすく はまこれ横浜
設定する 1 Nintendo Switchを無線ルーターから2~3mほどの位置に置きます。 無線ルーターから離れすぎていると接続できない場合があります。 2 HOMEボタンを押してHOMEメニューを表示し、「設定」を選びます。 3 「インターネット」→「インターネット設定」を選びます。 4ニンテンドーWiFiネットワークアダプタ （ニンテンドー・ワイファイ・ネットワーク・アダプタ）は、 任天堂 より販売されている ニンテンドーDS （以下DS）、 Wii 、 ニンテンドー3DS （以下3DS）、 Wii U 及び Nintendo Switch （以下Switch）向けの 無線LAN ルーター （ 無線LANアクセスポイント ）である。 任天堂 ニンテンドーWiFi ネットワークアダプタ WAPSWA全国各地のお店の価格情報がリアルタイムにわかるのは価格comならでは。製品レビューやクチコミもあります。
バーチャルコンソールで遊ぶ時に必要なものまとめ ゲームショップもこっそり紹介 ゼストゲーム班のブログ
英語学習リープパッドのソフト、ディズニーすすめ！オクトノーツステージ衣装やパーティー・結婚式衣装・イベントにどうぞリープパッド 英語 学習 ゲーム ソフト ディズニー すすめ オクトノーツ 理科 リープフロッグ 通販 Yahoo!ショッピング 『ディズニー ツムツム フェスティバル』は、「ディズニー ツムツム」のキャラクターたちと一緒に、パズルゲームやカーリング、ホッケーなど多彩な遊びが楽しめるパーティゲームでディズニーキャラクターとゲーム感覚で楽しくタイピングが学べる本格キーボード☆ ※マジカルスマートノート（別売）に接続して使う専用のキーボード＆ソフトのセットです。 マジカルスマートノート（別売）がないと遊べません。 キーボード JIS
Q Tbn And9gcqhf0766vqsxsqpl5blz6cqvtggc6h9wymla1chl2w8ts3jhuss Usqp Cau
13年 10月1日 、Wiiの生産終了を発表し、次世代機の Wii U に完全移行することとなった（廉価モデルである Wii Mini は生産継続）。 同年6月末までの累計販売台数は1億4万台に上り、同社の据え置き型としてはもっとも販売台数が多い機種になった 。 当時のドラゴンクエストX 目覚めし五つの種族 オンライン (Wii USBメモリー16GB同梱版) (封入特典ゲーム内アイテムのモーモンのぼうし同梱) 8,7 円 送料無料「Wii U/Wii用 USBメモリー16GB(Nintendo Wii U)」の商品情報やレビューなど。
Ps4 ゲームのセーブデータをコピーして別の本体に移す方法 ゲーム機の説明書
