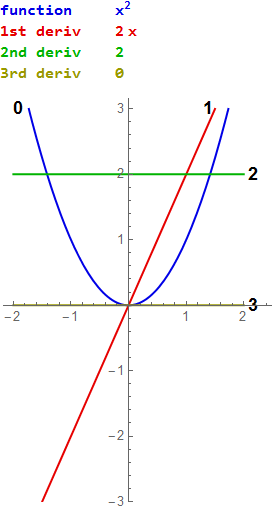
The derivative of a function y = f(x) of a variable x is a measure of the rate at which the value y of the function changes with respect to the change of the variable x It is called the derivative of f with respect to x If x and y are real numbers, and if the graph of f is plotted against x, the derivative is the slope of this graph at each point Problem Find the derivative of y =x^29 Plot the function and the derivative Solution Lets say you had the graph of just x^29 (without the absolute value, represented by the orange line in the graph below) that would look like the graph of x^2 shifted down 9 units y=(x2)(x2)(x4) graph{(x2)(x2)(x4) 10, 10, , } Fist we find the roots of the equation, ie the values of x st y=0 y=0 => (x2)(x2)(x4)=0 (1dp) These values of x correspond to the critical points (or turning points) we now use the second derivative to determine the nature (max, min or point of inflection) of these
Derivatives
